个人知乎:https://www.zhihu.com/people/kuingcry同步发布
前文链接:
RSA加密算法,从实际应用到基础原理(一)
上一篇文章的结尾处,我们提到了一个公式:
$$
\begin{Bmatrix}
m^e\ mod\ N = c\ (加密)
\end{Bmatrix}
$$
$$
\begin{Bmatrix}
c^d\ mod\ N = m\ (解密)
\end{Bmatrix}
$$
这个公式是RSA加密算法的核心,也是RSA加密算法的基础原理。
然而,这里我们并不会直接就进入RSA算法的解释,而是先来复习一些数论的知识。
A. 数论基础
1. 整除
如果整数n除以整数d的余数为0,就称d整除n,记作$d|n$。同时我们把d称为n的因数,n称为d的倍数。
2. 模运算
如果两个整数a和b除以n的余数相同,就称a,b模n同余,写作$a \equiv b\quad (mod\ n)$。
取模运算满足加法,减法和乘法,也就是说 如果有$a \equiv b\quad (mod\ n)$和$c \equiv d\quad (mod\ n)$,那么:
- $(a+c)\,\equiv\,(b+d)\quad (mod\ n)$
- $(a-c)\,\equiv\,(b-d)\quad (mod\ n)$
- $(ac)\,\equiv\,(bd)\quad (mod\ n)$
- $(a^n)\,\equiv\,(b^n)\quad (mod\ n)$
特殊的,对于除法,取模满足的性质是:
如果$ac\,\equiv\,bc\quad (mod\ n)$,那么:$a\,\equiv\,b\quad (mod\ \frac n {gcd(n,c)})$
在这里,如果n和c互质,那么$gcd(n,c) = 1$,可以得出$a\,\equiv\,b\quad (mod\ n)$
3. 最大公约数和最小公倍数
对于两个整数a和b,最大公约数是指能同时整除a和b的最大的正整数。最小公倍数是指能同时被a和b整除的最小的正整数。我们把最大公约数记作$gcd(a,b)$,把最小公倍数记作$lcm(a,b)$。
根据简单的数学推导,我们可以得到以下结论(a>b):
- $gcd(a,b) = gcd(b,a)$
- $gcd(ka,kb) = k\ gcd(a,b)$
- $gcd(k,ab) = 1 <--> gcd(k,a) = 1 \ and \ gcd(k,b) = 1$
- $gcd(a,b) = gcd(a-b,b)$
-
$gcd(a,b) = gcd(b,a\ mod\ b)$
我们可以使用欧几里得算法(Euclidean algorithm)来求解最大公约数。欧几里得算法利用了上面的第五条结论,即$gcd(a,b) = gcd(a\ mod\ b,b)$。
欧几里得算法的证明:
对于两个整数a和b,d是a和b的最大公约数的充要条件是:
$$
\begin{Bmatrix}
a = md\newline
b = nd\newline
(m和n的最大公约数为1)
\end{Bmatrix}
$$
又因为a可以写为$a = kb + r$,其中k是b的倍数,r是a除以b的余数,那么$r = a - kb = md - knd = (m-kn)d$。所以,只要证明n和$(m-kn)$的最大公约数为1,那么d就是b和r的最大公约数。假设n和$(m-kn)$有一个大于1的公约数p,那么$n = xp$,$m - kn = yp$,也就是$m = xkp + yp$。那么$m = (xk + y)p$,所以p也是m和n的公约数,因为p大于1,和前面的m和n的最大公约数为1矛盾,所以n和(m-kn)的最大公约数为1,也就是d是b和r的最大公约数。
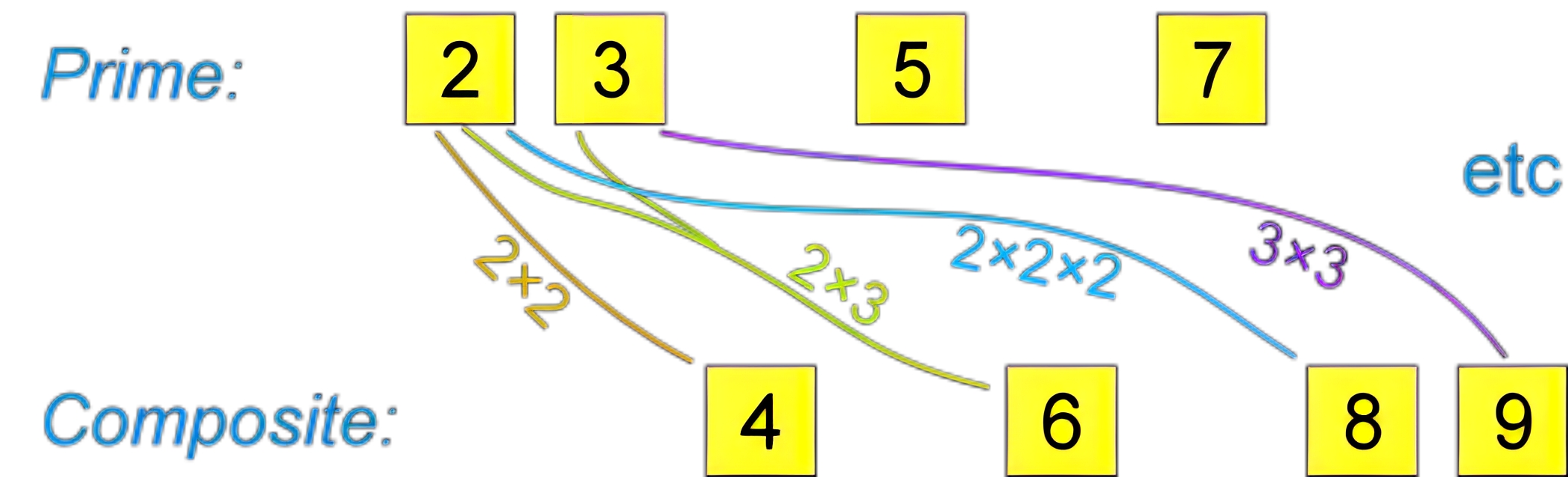
4. 质数与互质
一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,就称其为质数。
如果两个正整数,除了1以外,没有其他公约数,那么这两个数就是互质的。也就是$gcd(a,b)=1$。容易看出,这里的两个正整数,不一定都要是质数,比如8和9就是互质的。
根据互质的定义,我们可以推导出来以下结论:
- 1和任何正整数都是互质的。
- 如果有两个正整数a和b,a<b,且b是质数,那么a和b一定是互质的。
- 如果有大于1的整数p,那么p和p-1一定是互质的。
- 如果有大于1的奇数p,那么p和p-2一定是互质的。
- 任意两个质数一定是互质的。
- 如果一个数p是质数,另一个数只要不是p的倍数,那么这两个数一定是互质的。
6. 中国剩余定理
中国剩余定律,来自于《孙子算经》卷下的第26题:
今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
这是一个同余方程组:
$$
\begin{Bmatrix}
x \equiv 2(mod\ 3) \newline
x \equiv 3(mod\ 5) \newline
x \equiv 2(mod\ 7) \newline
\end{Bmatrix}
$$
将这个问题分解一下,其实我们只要找到三个整数,满足如下条件:
$$
\begin{Bmatrix}
x_1 \equiv 1(mod\ 3)\ \&\ x_1 \equiv 0(mod\ 5)\ \&\ x_1 \equiv 0(mod\ 7)\newline
x_2 \equiv 0(mod\ 3)\ \&\ x_2 \equiv 1(mod\ 5)\ \&\ x_2 \equiv 0(mod\ 7)\newline
x_3 \equiv 0(mod\ 3)\ \&\ x_3 \equiv 0(mod\ 5)\ \&\ x_3 \equiv 1(mod\ 7)\newline
\end{Bmatrix}
$$
那么根据我们前面提到过的模运算基本性质,那么$2x_1+3x_2+2x_3$就是我们要找的数。注意到这里的系数是方程组中的余数。
继续分解,对于$x_1$的求解,由于其可以被5和7整除,那么它一定是5×7=35的倍数,所以可以写成35k,也就是我们要求的其实就是满足$35k \equiv 1(mod\ 3)$的最小正整数k,扩展写法就是$ab \equiv 1(mod\ n)$,已知a和n的时候求解b。我们把b叫整数a对于模数n的模逆元,b存在的充分必要条件是a和n互质。这里k=2就是我们要求的解。
同样的求出其它两个解,那么最后的结果就是2×35×2+1×21×3+1×15×2=140+63+30=233。加法式的每一项都是(其他项模数的乘积对于余数的逆元)乘以(余数)乘以(其他项模数的乘积)。
注意到如果一个数x满足条件,那么x+105也满足条件,所以我们只要用233对于105取模,就可以得到最终的结果,结果为23。
推广到一般情况,如果有n个同余方程:
$$
\begin{Bmatrix}
x \equiv a_1(mod\ n_1)\newline
x \equiv a_2(mod\ n_2)\newline
\vdots\newline
x \equiv a_n(mod\ n_n)
\end{Bmatrix}
$$
对于上述方程,如果$n_1,n_2....n_n$两两互质,那么对于任意的正整数$a_1,a_2...a_n$,该方程组有解,设:
$$M=n_1n_2...n_n$$
并设:
$$M_i = \frac{M}{n_i}$$
同时
$t_i = M_i^{-1}$是$M_i$对于$n_i$的模逆元,那么方程组的解为:
$$x =\sum_{i=1}^n a_iM_it_i+kM$$
特别的,当$0<x<M$时,解x存在并唯一。
7. 欧拉函数
假如有一个正整数n,那么小于等于n且与n互质的正整数的个数,就称为n的欧拉函数,记作$\varphi(n)$。比如,$\varphi(10) = 4$,因为小于10且与10互质的正整数有4个:1,3,7,9。
根据上一部分我们根据互质的定义推导出的结论,让我们分情况讨论一下$\varphi(n)$的计算过程:
- 如果$n = 1$,那么$\varphi(1) = 1$。
- 如果n是质数,那么$\varphi(n) = n-1$,因为质数和小于它的每一个数都是互质的。
- 如果n是一个质数的幂次方,也就是说 $n=p^x$,那么$\varphi(n)=p^{x-1}(p-1)$,因为只有当一个数不是p的倍数的时候,它和n才是互质的。而p的倍数有$p,2p,3p,...,p^{(k-1)}p$,共有$p^{(k-1)}$个。所以,$\varphi(n) = p^x-p^{x-1} = p^{x-1}(p-1)=p^x(1-1/p)$。
-
如果一个质数可以写成两个互质的整数的乘积,也就是说$n=pq$,那么$\varphi(n) = \varphi(pq)$。这里我们需要证明一下欧拉函数是积性函数,也就是$\varphi(pq)=\varphi(p)\varphi(q)$。我们构造两个集合:
集合一:${a:1<=a<=pq,gcd(a,pq)=1}$
集合二:${(b,c):1<=b<=p,gcd(b,p)=1,1<=c<=q,gcd(c,q)=1}$。
可见第一个集合含有$\varphi(pq)$个元素,第二个集合含有$pq$个元素对。只要我们证明以下两个结论就能证明第一个集合的元素个数等于第二个集合的元素对个数:集合一中的不同元素对应集合二中的不同元素对。
集合二中的每个元素对都对应集合一中的一个不同元素。第一点可以使用反证法得证,而第二点就可以使用我们上面提到的中国剩余定律,构造同余式进行证明。
-
根据唯一分解定理,任意一个正整数都可以写成若干个质数的乘积,也就是说
$$
n = p_1^{k1}p_2^{k2}p_3^{k3}...p_r^{kr}
$$那么$\varphi(n)=\varphi(p_1^{k1})\varphi(p_2^{k2})\varphi(p_3^{k3})...\varphi(p_r^{kr})$,再根据上面的结论,我们可以得到
$$
\begin{Bmatrix}
\varphi(n) = (p_1^{k1}-p_1^{k1-1})(p_2^{k2}-p_2^{k2-1})...(p_r^{kr}-p_r^{kr-1})\newline
= p_1^{k1}(1-1/p_1)p_2^{k2}(1-1/p_2)...p_r^{kr}(1-1/p_r)\newline
=n(1-1/p_1)(1-1/p_2)...(1-1/p_r)
\end{Bmatrix}
$$
这就是欧拉函数的一般求解公式。
8. 欧拉定理
前面我们已经知道了欧拉函数的定义和一般求解公式,现在我们来看一下欧拉定理。欧拉定理是指,如果一个数a和n互质,那么
$$
a^{\varphi(n)}\equiv 1 (mod\ n)
$$
也就是说,如果一个数a和n互质,那么$a^{\varphi(n)}$模n的余数为1。
特殊的,如果n是质数,那么$\varphi(n)=n-1$,这时欧拉定理可以写成
$$
a^{(n-1)}\equiv 1 (mod\ n)
$$
B. RSA算法的原理
1. RSA算法的计算过程
前面说了这么多公式,现在我们终于可以回到RSA算法了,先来再看一遍RSA加密的公式:
$$
\begin{Bmatrix}
m^e\ mod\ N = c\ (加密)
\end{Bmatrix}
$$
$$
\begin{Bmatrix}
c^d\ mod\ N = m\ (解密)
\end{Bmatrix}
$$
其中:N,e,d,p,q,这5个数字是我们之前在公私钥文件里发现的,m是我们要加密的信息(将信息使用ASCII编码或Unicode编码转化为一串数字,然后切割成短于N的一系列数字),c是加密后的信息。
那么,RSA算法的计算过程如下:
- 选择两个不同的质数p和q,其中p和q要越大越好,因为p和q越大,N就越大,也就约难以破解。
- 计算N,N=pq。我们第一篇文章里在公私钥文件里发现的N就是这个N。其位数是2048位,也就是说,RSA算法的安全性是2048位。
- 计算欧拉函数$\varphi(N)$,$\varphi(N)=\varphi(p)\varphi(q)=(p-1)(q-1)$
- 随便选择一个数e,要求e和$\varphi(N)$互质,且e要小于$\varphi(N)$,这样我们就可以计算出d,d是e的模$\varphi(N)$的乘法逆元,也就是说,
$$ed\equiv 1 (mod\ \varphi(N))$$
我们第一篇文章里在公私钥文件里发现的e就是这个e,d就是这个d。这里求逆元可以使用扩展欧几里得算法。 - 把N和e写入公钥文件,把N和d写入私钥文件。这时候,我们就可以使用公钥文件对信息进行加密了。
- 用私钥文件对加密后的信息进行解密,得到原信息。
2. RSA算法的证明
前面,我们已经知道了RSA算法的计算过程,现在我们来证明一下为什么用e加密后的信息c,用d解密后能还原成原信息m。也就是说,我们要证明$c^d\ \equiv m\ (mod\ N)$。因为加密过程是$m^e\ mod\ N = c$,所以$c=m^e+kN$,其中k是一个整数。那么,把c带入上面的解密公式,可以看出我们要证明的就是:
$$(m^e+kN)^d\equiv m\ (mod\ N)$$
我们容易看出左边的展开项除了$m^{ed}$之外,其他项都带有N,所以我们只需要证明
$$m^{ed}\equiv m\ (mod\ N)$$
这样我们就证明了$c^d\ \equiv m\ (mod\ N)$。因为
$$ed\equiv 1 (mod\ \varphi(N))$$
所以,$ed = k\varphi(N)+1$,那么$m^{ed} = m^{k\varphi(N)+1}$,也就是我们要证明
$$m^{k\varphi(N)+1}\equiv m\ (mod\ N)$$
如果m和N互质,那么根据欧拉定律,$m^{\varphi(N)}\equiv 1\ (mod\ N)$,所以
$$m^{k\varphi(N)+1}\equiv m^{k\varphi(N)}m\equiv (1)^km\equiv m\ (mod\ N)$$
如果m和N不互质,因为$N=p*q$,所以这种情况下m一定是p或q的倍数,那么我们以$m=kp$为例,考虑到$m<N=pq$,所以$k<q$,那么这时候一定有k和q互质,所以kp和q互质,所以
$$(kp)^{\varphi(q)}\equiv (kp)^{q-1}\equiv 1\ (mod\ q)$$
因为
$$ed = k\varphi(N)+1 = k(\varphi(p)\varphi(q))+1 = k(p-1)(q-1)+1$$
所以
$$(kp)^{ed} = (kp)^{k(p-1)(q-1)+1} = (kp)^{k(p-1)(q-1)}(kp)^1 = {(kp)^{q-1}}^{k(p-1)}(kp)^1$$
所以
$$(kp)^{ed} \equiv kq\ (mod\ q)$$
也就是
$$(kp)^{ed} = k_2q + kp$$
因为kp和q互质,所以这里的$k_2$一定是p的倍数,也就是$k_2q = k_3pq$,所以
$$(kp)^{ed} = k_3pq + kp$$
因为$N=pq$,$m=kp$,所以
$$m^{ed} = k_3N + m$$
也就是
$$m^{ed}\equiv m\ (mod\ N)$$
得证
3. RSA算法的安全性
我们已经知道了RSA算法的计算过程,也证明了加解密过程的正确性,那么,RSA算法的安全性是怎么保证的呢?
我们知道,RSA算法的加密过程是$c=m^e\ mod\ N$,解密过程是$m=c^d\ mod\ N$,那么,已知N和e,能否推导出d?如果能推导出d,那么就等于私钥泄漏,那么RSA算法就不安全了。因为$ed\equiv 1\ (mod\ \varphi(N))$,所以我们要知道e和$\varphi(N)$,才能算出d。又因为$\varphi(N) = (p-1)(q-1)$,所以我们必须知道p和q,同时$N=pq$,所以只要能把n因数分解出p,q,我们就破解了RSA算法。
可是,大整数的因数分解,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。
比如我们可以很容易的算出下面的结果
$$
\begin{Bmatrix}
1314517 * 1314527 = 1727968088459
\end{Bmatrix}
$$
但当我们去反向把1727968088459分解为质因数的乘积时就会明显比正向计算时耗费更多的功夫,而且对于越大的数,我们就越难去分解它。
大数分解是一个NP问题,P=NP? 这可能是计算机数学中最难的问题。
后续有时间可以再单独介绍下。
事实上,目前被破解的RSA密码最长为795位,然而我们这里用的都2048位了,可见其安全性之高。当然,破解RSA算法还存在一种情况,因为RSA算法是确定性算法,所以,如果我们能够预先知道明文的分布范围,比如6位数数字组成的密码,那么我们就可以通过暴力破解的方式,得到明文,从而得到密钥。所以,一般情况下,我们会在明文前后加上一些随机字符,使得明文的长度达到一定的要求,这样,即使我们知道明文的分布范围,也很难通过暴力破解的方式得到明文。





Comments NOTHING